A Quantum Algorithm for Dense Kernel Matrices Using Hierarchical Splittings

Quynh The Nguyen | Bobak Toussi Kiani | Seth Lloyd

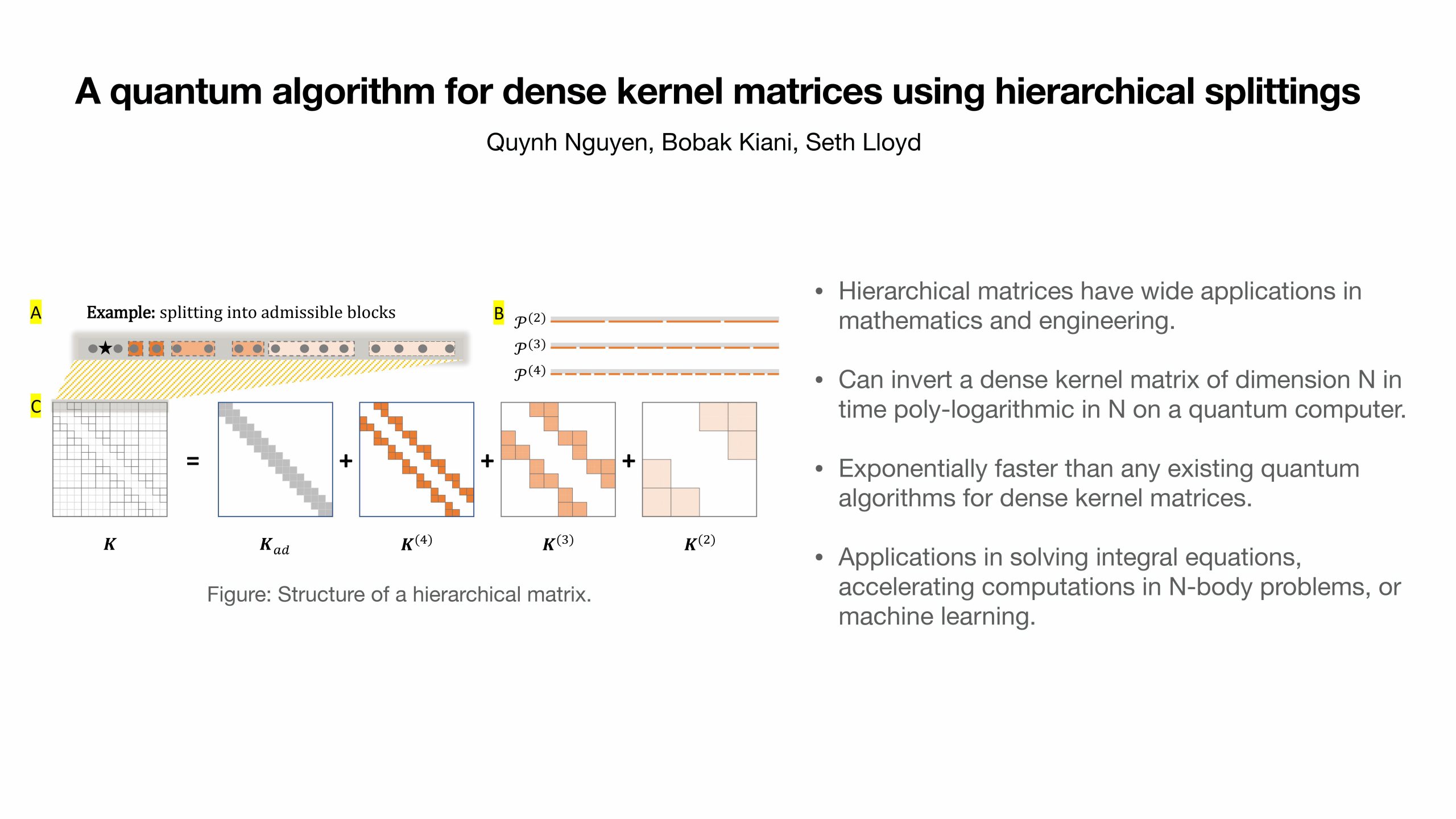
Kernel matrices, which arise from discretizing a kernel function, have a variety of applications in mathematics and engineering. Due to their structured form, much research has been devoted to accelerating matrix operations on kernel matrices. Most notably, the celebrated fast multipole method algorithm showed that classically, one can perform matrix multiplication on kernel matrices of dimension N in time almost linear in N by implementing the matrix as a hierarchical matrix. In light of this success, we propose a quantum algorithm for efficiently performing matrix operations on hierarchical matrices by implementing a quantum block-encoding of the hierarchical matrix structure. Our quantum algorithm can perform matrix inversion of kernel matrices of dimension N in time polylogarithmic in N and the target error, as well as linear in the condition number of the matrix. This runtime is exponentially faster than any existing quantum algorithms for implementing dense kernel matrices. We also discuss possible applications of our algorithm in solving integral equations or accelerating computations in N-body problems.

Funding Sources: This work was supported by the NSF, IARPA, DOE, and DARPA.